Skewness And Kurtosis Values To Determine Normality In Spss

Skewness and kurtosis are two moment based measures that will help you to quickly calculate the degree of departure from normality.

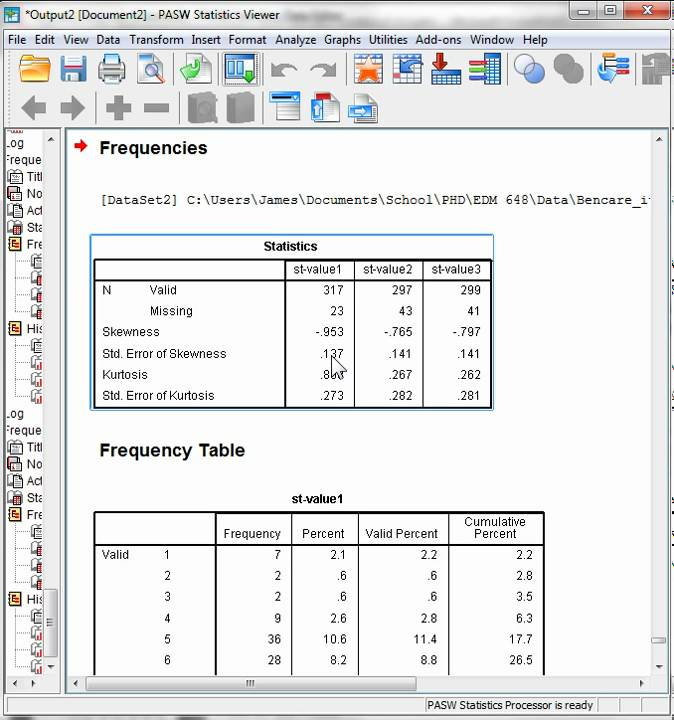
Skewness and kurtosis values to determine normality in spss. This suggests that they are not normally distributed in the entire population. This distribution has kurtosis statistic similar to that of the normal distribution it means that the extreme values of the distribution are similar to that of a normal distribution characteristic. You can learn more about our enhanced content on our features. Calculate skewness and kurtosis.

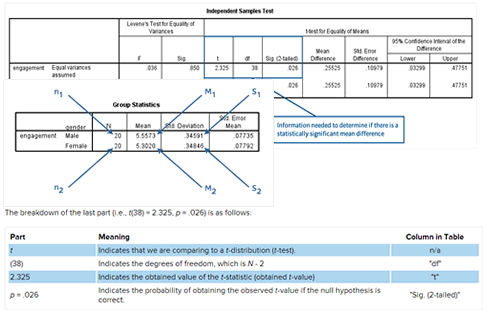
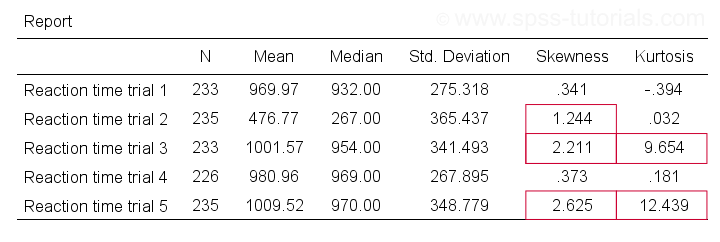
Trials 2 3 and 5 all have a huge skewness and or kurtosis. Spss runs two statistical tests of normality kolmogorov smirnov and shapiro wilk. The result suggested the deviation of data from normality was not severe as the value of skewness and kurtosis index were below 3 and 10 respectively kline 2011. In addition to using skewness and kurtosis you should use the omnibus k squared and jarque bera tests to determine whether the amount of departure from normality is statistically significant.

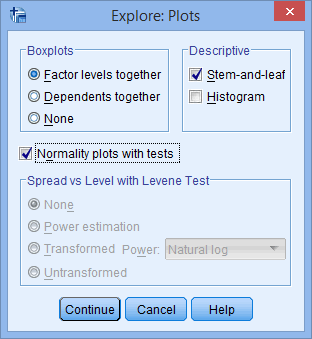
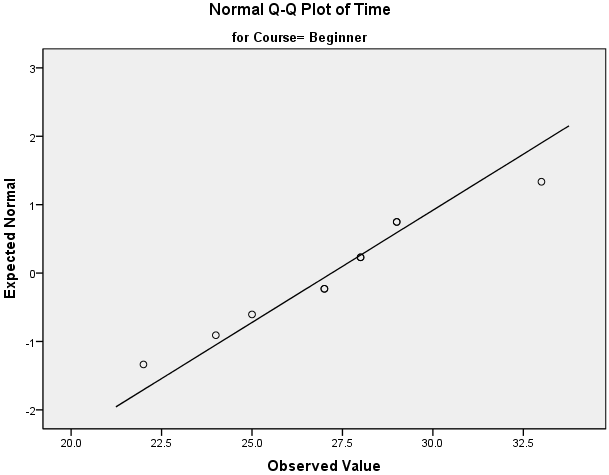
Hit ok and check for any skew values over 2 or under 2 and any kurtosis values over 7 or under 7 in the output. The usual reason to do this is to get an idea of whether the data is normally distributed. If it is below 0 05 the data significantly deviate from a normal distribution. If you need to use skewness and kurtosis values to determine normality rather the shapiro wilk test you will find these in our enhanced testing for normality guide.

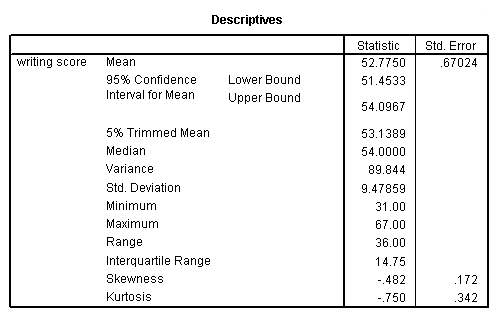
Source yadav r pathak g. There are a number of different ways to calculate skewness and kurtosis in spss. In spss the skewness and kurtosis statistic values should be less than 1 0 to be considered normal. Skewness and kurtosis are closer to zero for trials 1 and 4.

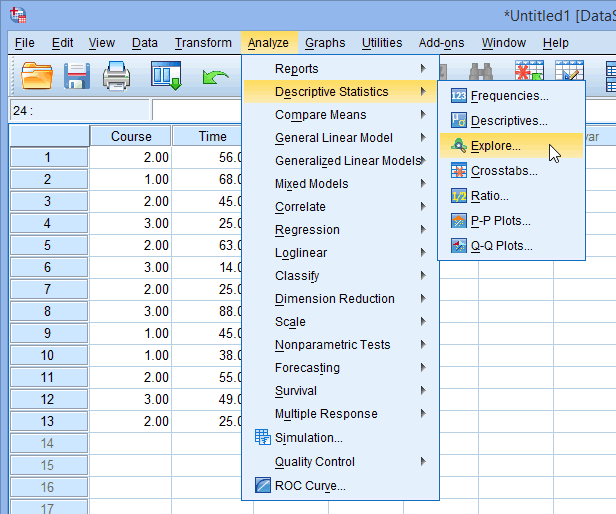
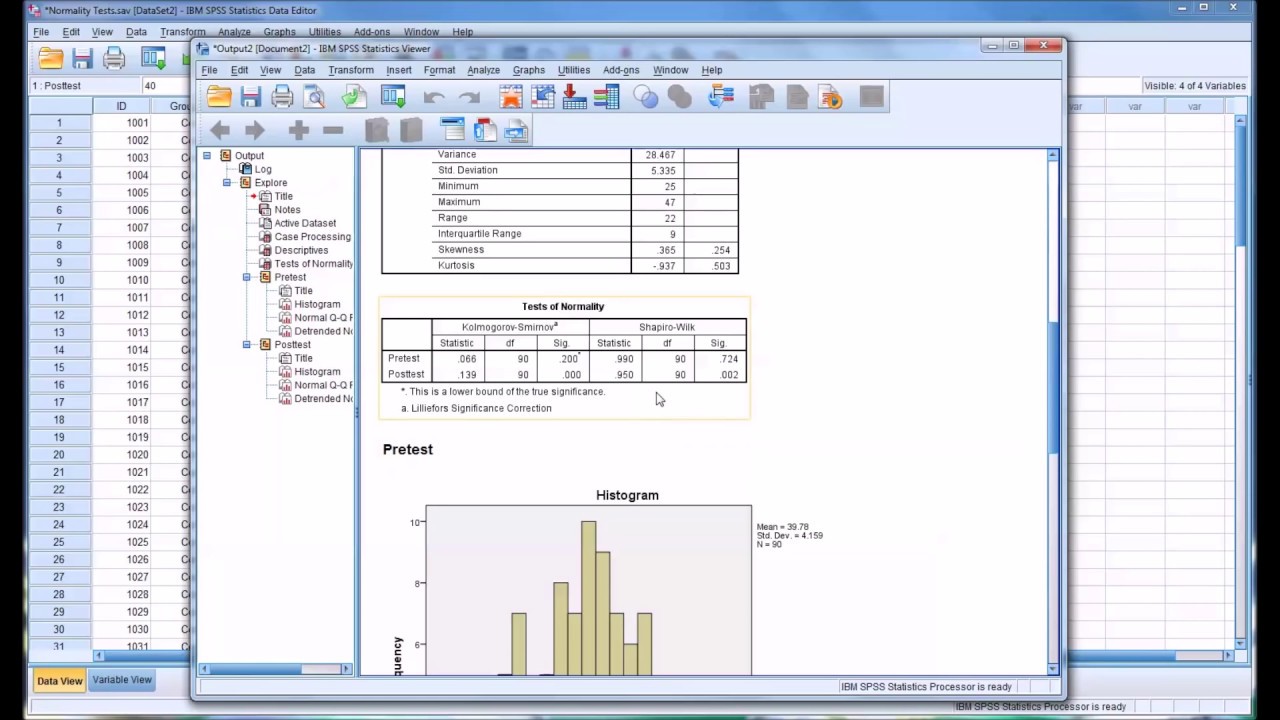
Running the shapiro wilk test in spss. We re going to calculate the skewness and kurtosis of the data that represents the frisbee throwing distance in metres variable see above. This definition is used so that the standard normal distribution has a kurtosis of three. Distribution is longer tails are fatter.

Leptokurtic kurtosis 3. Those values might indicate that a variable may be non normal. If the significance value is greater than the alpha value we ll use 05 as our alpha value then there is no reason to think that our data differs significantly from a normal distribution i e we can reject the null hypothesis that it is non normal. For skewness if the value is greater than 1 0 the distribution is right skewed.

Kurtosis tells you the height and sharpness of the central peak relative to that of a standard bell curve. Here x is the sample mean. Clicking on options gives you the ability to select kurtosis and skewness in the options menu. The minus 3 at the end of this formula is often explained as a correction to make.